industriesjilo.blogg.se - Quadratic function in standard form

Note, that the value of 'b' can also be a zero. In the standard form of quadratic equation ax 2 + bx + c = 0, only 'a' has a restriction that it should not be a zero. Can 'c ' be a Zero in the Standard Form of Quadratic Equation? The standard form of a quadratic equation with variable x is expressed as ax 2 + bx + c = 0, where a, b, and c are constants such that 'a' is a non-zero number but the values of 'b' and 'c' can be zeros. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.įAQs on Standard Form of Quadratic Equation What is Quadratic Standard Form? Our mission is to transform the way children learn math, to help them excel in school and competitive exams.

A quadratic equation in intercept form is a (x - p)(x - q) + k = 0, where p and q are the roots of the quadratic equation.Ĭuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12.

A quadratic equation in vertex form is a (x - h) 2 + k = 0, where h = -b/2a and k = (4ac - b 2) / (4a).

A quadratic equation in standard form is ax 2 + bx + c = 0.

Important Notes on Standard Form of Quadratic Equation: Let us consider the above example (x - 1) (2x - 5) = 0 and let us convert it back into standard form. The process of converting the intercept form of a quadratic equation into standard form is really easy and it is done by simply multiplying the binomials (x - p) (x - q) and simplifying. (x - 1) (2x - 5) = 0 Converting Intercept Form to Standard Form Now we will solve the quadratic equation by factorization.

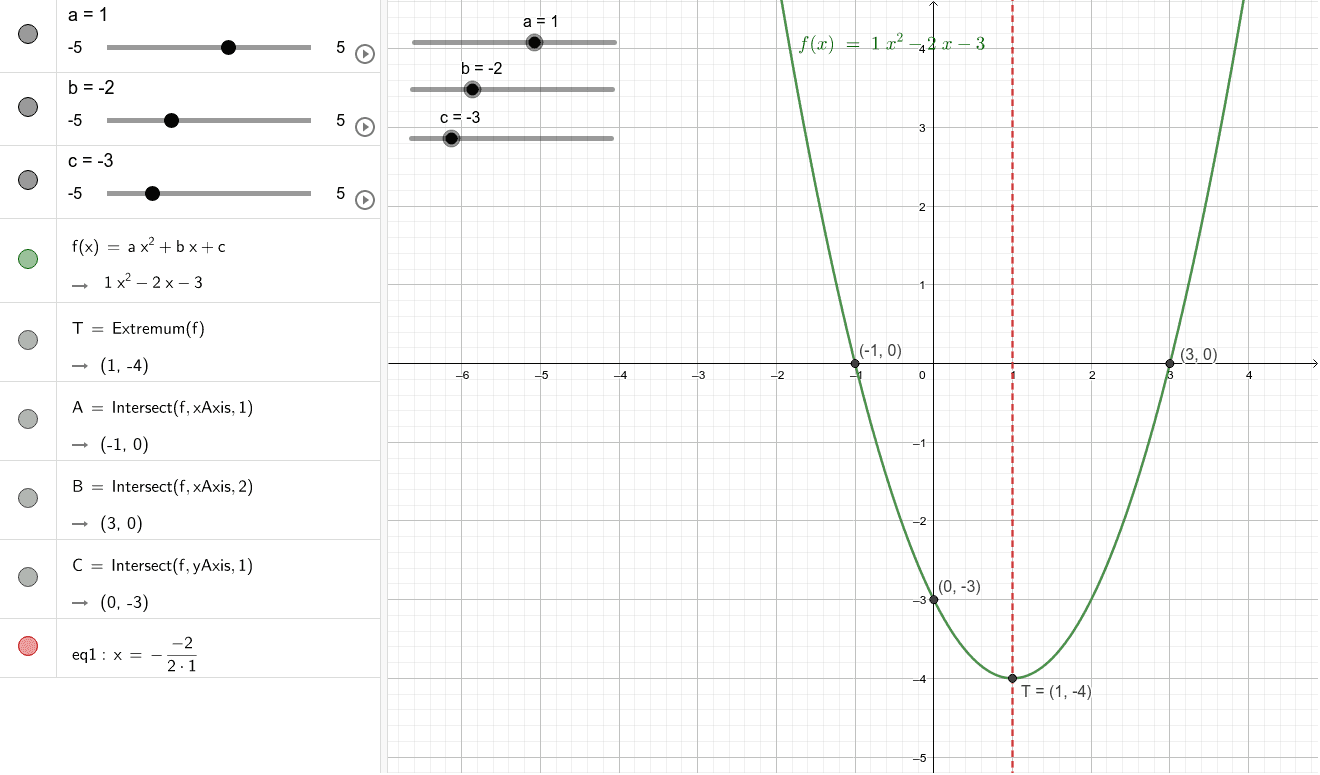
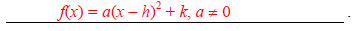
By comparing this with ax 2 + bx + c = 0, we get a = 2. Example to Convert Standard to Intercept FormĬonsider the quadratic equation in standard form 2x 2 - 7x + 5 = 0. Thus, we just use any one of the solving quadratic equation techniques to find p and q. Here, (p, 0) and (q, 0) are the x-intercepts of the quadratic function f(x) = ax 2 + bx + c) and hence p and q are the roots of the quadratic equation. Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - p)(x - q) = 0. Let us consider the above example 2 (x - 1) 2 + 1 = 0 and let us convert it back into standard form.Ģx 2 - 4x + 3 = 0 -> Standard FormĬonverting Standard Form of Quadratic Equation into Intercept Form The process of converting the vertex form of a quadratic equation into the standard form is pretty simple and it is done by simply evaluating (x - h) 2 = (x - h) (x - h) and simplifying. Substituting a = 2, h = 1, and k = 1 in the vertex form a (x - h) 2 + k = 0, we get:Ģ (x - 1) 2 + 1 = 0 Converting Vertex Form to Standard Form To convert it into the vertex form, let us find the values of h and k. Comparing this with ax 2 + bx + c = 0, we get a = 2, b = -4, and c = 3. Example of Converting Standard Form to Vertex FormĬonsider the quadratic equation 2x 2 - 4x + 3 = 0. Thus, we can use the formulas h = -b/2a and k = (4ac - b 2) / (4a) to convert the standard to vertex form. Let us just set them equal to know the relation between the variables.Īx 2 + bx + c = ax 2 - 2ah x + (ah 2 + k)Ĭomparing the coefficients of x on both sides, Note that the value of 'a' is the same in both equations. Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - h) 2 + k = 0 (where (h, k) is the vertex of the quadratic function f(x) = a (x - h) 2 + k). Converting Standard Form of Quadratic Equation into Vertex Form The axes of symmetry of the parabolas are the vertical lines with equations x = 5 0 and x = 6 5. Use a calculator to evaluate the equations if necessary. The axis of symmetry is given by the equation x = 2 a - b , where a is the coefficient of the x 2 -term and b is the linear coefficient. Reflect the y -intercept in the axis of symmetry.Identify and graph the axis of symmetry.To do so, there are five steps to follow. The functions can now be graphed using the standard form. By following the same procedure, the second function that represents Sugoi Sketch can also be rewritten in standard form.